Для профессионального электрика и электронщика Закон Ома является необходимым инструментом при выполнении задач по наладке, настройке и ремонту электронных и электрических схем.
Каждый нуждается в понимании этого закона, так как каждый использует электричество в повседневной жизни.
Несмотря на то что курс средней школы предусматривает изучение закона немецкого физика Ома, практика показывает, что этот закон не всегда осваивается своевременно. В нашем материале рассмотрим актуальную тему и разберемся с вариантами записи формулы.
Раздельное место и полноценный электропроводящий путь.
Применительно к закону Ома в электрической цепи возможно два подхода к расчету: для отдельного участка или для всей цепи.
Вычисление силы тока в участке электроцепи.
В схеме обычно изучают участок цепи без источника ЭДС, так как его считают частью с собственным сопротивлением.
В этом случае расчетная формула представляет собой простое выражение.
I = U/ R,
Где, соответственно:
- I – сила тока;
- U – приложенное напряжение;
- R – сопротивление.
Формула выражает простое явление: сила тока в участке цепи прямо пропорциональна напряжению на нём и обратно пропорциональна сопротивлению.
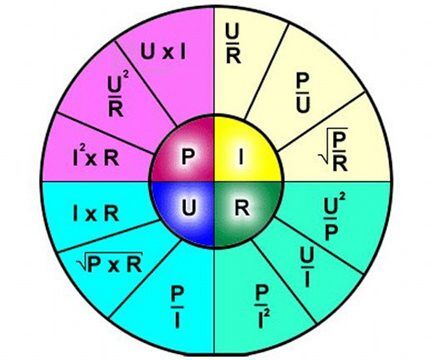
Формула точно отображает взаимосвязь протекающего тока на участке электрической цепи с заданными значениями напряжения и сопротивления.
Формулу можно применять для расчета параметров сопротивления, необходимых для схемы при известном напряжении и токе.
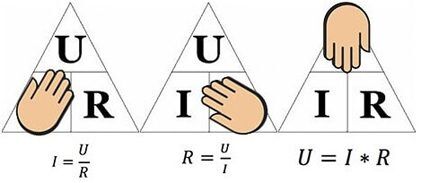
Рисунок помогает определить ток, протекающий через сопротивление в 10 Ом при напряжении 12 вольт. Подставляя значения, получим: I = 12 / 10 = 1.2 ампера.
Поиск сопротивления при известных токе и напряжении, а также поиск напряжения при известных токе и напряжении решаются аналогичным образом.
Таким образом, можно выбрать нужное рабочее напряжение, необходимый ток и наилучший резистор.
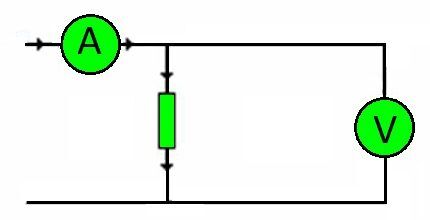
Соединительные провода в любой схеме представляют собой сопротивления. Размер нагрузки, которую им предстоит выдержать, устанавливается напряжением.
Следуя закону Ома, можно точно подобрать сечение проводника, исходя из материала его жилы.
У нас на сайте есть подробная инструкция по расчету сечения кабеля по мощности и току.
Вариант расчета для полной цепи
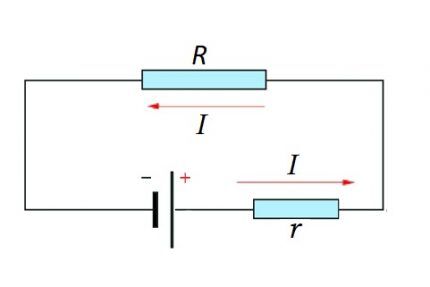
Чтобы получить полноценную цепь, требуется участком (участками) и источником ЭДС. В действительности к существующему в цепи резистивному элементу присоединяется внутреннее сопротивление источника ЭДС.
Следовательно, целесообразно внести коррективы в ранее проанализированную формулу.
I = U / (R + r)
Значение внутреннего сопротивления ЭДС в законе Ома для полного электрического circuits можно пренебречь, хотя оно всё же связано с конструкцией источника ЭДС.
При вычислении сложных электронных схем и электрических цепей с большим количеством проводников добавочное сопротивление имеет значение.
При рассмотрении как отдельного звена цепи, так и всей системы важно принимать во внимание характер применяемого тока: постоянный или переменный.
Применительно к переменному току упомянутые особенности закона Ома проявляются по-другому.
Анализ влияния законодательства на изменяющуюся величину.
Понятие «сопротивление» при прохождении переменного тока лучше всего понимать как «импеданс», представляющий собой сочетание активной резистивной нагрузки (Ra) и нагрузки, созданной реактивным резистором (Rr).
Такие явления определяют параметры индуктивных элементов и законы коммутации для переменного напряжения, то есть для синусоидального тока.
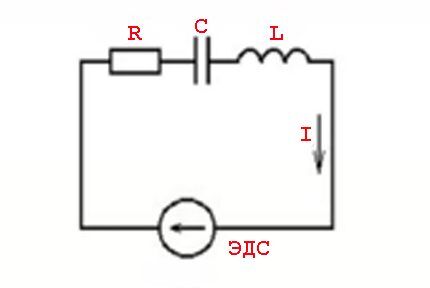
Токовые значения могут опережать (отставать) по сравнению с напряжениями, приводя к появлению активной и реактивной мощностей.
Вычисление таких процессов выполняется по следующей формуле:
Z = U / I или Z = R + J * (XL — XC)
где: Z – импеданс; R – активная нагрузка; XL , XC – индуктивная и емкостная нагрузка; J – коэффициент.
Последовательное и параллельное включение элементов
Электрические цепи состоят из участков, соединенных последовательно или параллельно.
Каждый тип соединения характеризуется собственным режимом протекания тока и подачей напряжения. В связи с этим закон Ома используется с различной точностью, исходя из схемы подключения элементов.
Последовательное соединение резисторов.
Для последовательного соединения (отрезка цепи, состоящего из двух компонентов), применяется следующее выражение:
- I = I1 = I2 ;
- U = U1 + U2 ;
- R = R1 + R2
Формулировка ясно показывает, что значение тока в участке цепи остается неизменным при любом количестве последовательно подключенных резисторов.
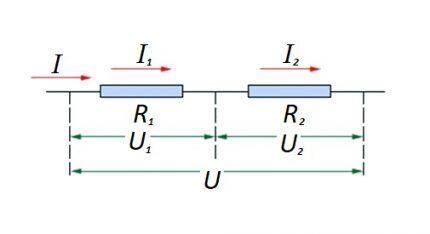
Напряжение, подаваемое на активные элементы схемы, равно величине источника тока.
В таком случае напряжённость каждого элемента равна: Ux = I * Rx.
Полное сопротивление получается суммой значений всех сопротивлений в электрической цепи.
Параллельно соединенные резисторы.
При одновременном использовании резисторов применима формула, предложенная немецким физиком Омом.
- I = I1 + I2 … ;
- U = U1 = U2 … ;
- 1 / R = 1 / R1 + 1 / R2 + …
Возможны схемы с комбинированным типом соединения элементов: как параллельным, так и последовательным.
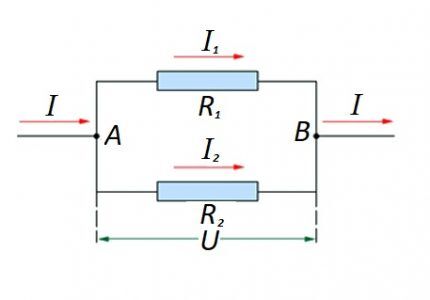
Расчет для таких случаев производится исходя из первоначального значения сопротивления параллельно соединенных элементов. К полученному значению прибавляется сопротивление последовательно подключенного резистора.
Интегральная и дифференциальная формы закона
Все расчеты, указанные ранее, справедливы для электрических схем с однородными проводниками.
На практике часто создаются схемы, в которых конструкция проводов изменяется по протяжённости трассы. В качестве примера можно привести использование проводов разного сечения или изготовленных из различных материалов.
Чтобы учесть эти отличия, используется вариант, называемый «дифференциально-интегральным законом Ома». Для бесконечно малого проводника определяется уровень плотности тока на основе напряжённости поля и удельной проводимости.
Под дифференциальный расчет берется формула: J = ό * E
Для интегрального расчета, соответственно, формулировка: I * R = φ1 – φ2 + έ
Эти примеры больше подходят для высшей математики, а в работе обычного электрика практически не используются.
Выводы и полезное видео по теме
Видеоролик ниже даст полное представление о законе Ома.
Видеоурок наглядно дополняет теоретический материал, представленный в письменном виде.

Профессия электрика и электронщика предполагает непосредственное столкновение с законом Ома. Это базовая информация, необходимая всем специалистам.
Для успешного применения достаточно изучить три основных варианта формулировки вопроса.
Хотите поделиться своим мнением по данной статье? Напишите комментарий ниже. Возникли вопросы? Не стесняйтесь обратиться к нашим экспертам.